3 Rekursion

Forståelse af rekursion er en forudsætning for at forstå et eksempel i afsnit 4.7.3. Derudover forudsættes kapitlet ikke i resten af bogen.

Rekursion er velegnet, hvis en opgave kan deles op i mindre tilsvarende delopgaver.

3.1 Introduktion til rekursive algoritmer

Hvis en metode kalder sig selv, er der tale om rekursion. F.eks.:

public class Rekursion
{
  public static void main(String[] arg)
  {
    tælNed(3);
  }

  public static void tælNed(int tæller)
  {
    System.out.print(tæller+" ");
    if (tæller>0) tælNed(tæller-1); // tælNed() kalder sig selv !!
  }
}

3 2 1 0

Fidusen er, at tæller-parameteren eksisterer én gang for hver gang, tælNed() bliver kaldt. Så når tælNed() vender tilbage til kalderen, som også er tælNed(), er tællers værdi bevaret som før kaldet.

3.1.1 Folde en rekursion ud

Er man uvant med rekursion, kan det være svært at gennemskue, hvad der sker. Husk da, at et kald til en metode er uafhængigt af, om metoden eventuelt allerede "er i gang med" at blive kaldt. Ovenstående rekursion kunne "foldes ud" til følgende program:

public class RekursionUdfoldet
{
  public static void main(String[] arg)
  {
    tælNed(3);
  }

  public static void tælNed(int tæller)
  {
    System.out.print(tæller+" ");
    if (tæller>0) tælNedA(tæller-1);    // kald tælNedA(2)
  }

  public static void tælNedA(int tæller)
  {
    System.out.print(tæller+" ");
    if (tæller>0) tælNedB(tæller-1);    // kald tælNedB(1)
  }
 
  public static void tælNedB(int tæller)
  {
    System.out.print(tæller+" ");
    if (tæller>0) tælNedC(tæller-1);    // kald tælNedC(0)
  }

  public static void tælNedC(int tæller)
  {
    System.out.print(tæller+" ");
    if (tæller>0) tælNedC(tæller-1);    // kalder ikke videre, da tæller=0
  }
}

3 2 1 0

Det er klart, at rekursion nemt kan føre til uendelige løkker, hvis man ikke passer på.

3.1.2 Forudsætninger for rekursion

Man kan groft sagt være sikker på, at der ikke opstår en uendelig løkke, hvis man kan påvise, at alle videre kald sker med en mindre opgave end der blev kaldt med, og at en tilstrækkelig lille opgave bliver udført uden et videre kald.

Herover bliver opgaven mindre og mindre, fordi tæller bliver reduceret med 1 i hvert kald, og fordi tælNed() kun kalder sig selv, hvis tæller er større end 0.

Rekursion kan løse en slags opgave hvis:

1. Opgaven kan deles om i mindre bidder af samme karakter som den oprindelige opgave

2. En tilstrækkelig lille opgave altid kan løses

3.2 Rekursiv listning af filer

Her ses et andet eksempel på rekursion, hvor filer i det aktuelle katalog og alle underkataloger listes rekursivt.

Klassen File, der repræsenterer en fil eller et katalog, kan bruges til at navigere i filsystemet, slette eller omdøbe filer eller kataloger og aflæse eller sætte deres attributter.

Det følgende eksempel lister alle filerne i det aktuelle katalog. Er der nogle underkataloger, listes indholdet af dem også (rekursionen består i, at listKatalog() kalder sig selv).

import java.io.*;
public class ListFilerRekursivt
{
  public static void main(String[] arg)
  {
    File kat = new File(".");   // objekt der repræsenterer det aktuelle katalog
    listKatalog(kat);
  }

  private static void listKatalog(File kat)
  {
    File[] filer = kat.listFiles();

    for (int i=0; i<filer.length; i++) 
    {
      File f = filer[i];

      if (f.isDirectory())
      {
        System.out.println("Katalog "+f+":");
        listKatalog(f);                         // kald listKatalog() rekursivt
        System.out.println("Katalog "+f+" slut.");
      } else {
        System.out.println(f);                  // udskriv filens navn og sti
      }
    }
  }
}

./ListFilerRekursivt.class
./ListFilerRekursivt.java
Katalog ./Desktop:
./Desktop/Home.desktop
./Desktop/MandrakeClub.desktop
Katalog ./Desktop/Removable media:
./Desktop/Removable media/Floppy
./Desktop/Removable media/CD-ROM
Katalog ./Desktop/Removable media slut.
Katalog ./Desktop/Affald:
Katalog ./Desktop/Affald slut.
Katalog ./Desktop slut.
Katalog ./tmp:
Katalog ./tmp slut.

Programmet er startet fra et katalog, der indeholdt ListFilerRekursivt.java og ListFilerRekursivt.class og underkatalogerne Desktop (der igen indeholdt bl.a. Home.desktop, MandrakeClub.desktop og underkatalogerne Removable media og Affald) og tmp.

3.3 Beregning af et matematisk udtryk

Det følgende program kan analysere en streng og udregne et matematisk udtryk med de fire regnearter, sinus-funktionen og et vilkårligt antal parenteser.

public class Formelberegning
{
  /**
   * Finder første position af en operator, f.eks. +, -, * eller /.
   * Går uden om de operatorer, der er inde i en parentes.
   * Simpel løsning, der ikke tager højde for parenteser: udtryk.indexOf(tegn)
   */
  private static int findUdenforParenteser(char tegn, String udtryk)
  {
    int par = 0;
    for (int i = 0; i<udtryk.length(); i++)
    {
      char t = udtryk.charAt(i);
      if (t == tegn && par==0) return i; // tegn fundet udenfor parenteser!
      else if (t == '(') par++;          // vi går ind i en parentes
      else if (t == ')') par--;          // vi går ud af en parentes
    }
    return -1; // tegnet blev ikke fundet (i hvert fald ikke udenfor parenteser)
  }


  /**
   * Beregner værdien at et udtryk.
   * @param udtryk En streng med udtrykket, der skal beregnes.
   * @return værdien af udtrykket.
   * @throws NumberFormatException hvis udtrykket ikke er gyldigt
   */
  public static double beregn(String udtryk)
  {
    udtryk = udtryk.trim();                  // fjern overflødige blanktegn
    for (int opNr = 0; opNr < 4; opNr++)     // løb gennem de fire regnearter
    {
      char op = "+-*/".charAt(opNr);         // op er nu '+', '-', '*' eller '/'
      int pos = findUdenforParenteser(op,udtryk);
      if (pos > 0)                           // findes op i udtrykket?
      {
        String vs = udtryk.substring(0,pos); // ja, find venstresiden
        String hs = udtryk.substring(pos+1); // find højresiden

        // metoden kalder nu sig selv og analyserer hvert element i strengen
        double vsr = beregn(vs);             // beregn højresidens værdi
        System.out.println("beregn("+vs+") = "+vsr);
        double hsr = beregn(hs);             // beregn venstresidens værdi
        System.out.println("beregn("+hs+") = "+hsr);

        if (op == '+') return vsr + hsr;     // beregn resultat og returnér
        if (op == '-') return vsr - hsr;
        if (op == '*') return vsr * hsr;
        return vsr / hsr;
      }
    }
    // Hvis vi kommer herned kunne der ikke dele op i flere operatorer
    if (udtryk.startsWith("(") && udtryk.endsWith(")"))   // parenteser omkring?
    {
      udtryk = udtryk.substring(1,udtryk.length()-1);     // fjern dem
      return beregn(udtryk);                              // beregn indmad
    }
    if (udtryk.startsWith("sin(") && udtryk.endsWith(")"))// sinus-funktion
    {
      udtryk = udtryk.substring(4,udtryk.length()-1);     // fjern 'sin(' og )
      double resultat = beregn(udtryk);                   // beregn parameteren
      System.out.println("beregn("+udtryk+") = "+resultat);
      return Math.sin(resultat);
    }
    // intet andet fundet - så må det være et tal! 
    // (ellers kastes NumberFormatException)
    return Double.parseDouble(udtryk);
  }

  public static void main(String[] arg)
  {
    String formel = "(1+2)*3 - sin(4/5*(6-7))";
    double værdi = beregn(formel);
    System.out.println("Formlen "+formel+" er beregnet til "+værdi);
  }
}

Herunder ses udskriften fra programmet ved udregning af "(1+2)*3 - sin(4/5*(6-7))":

beregn(1) = 1.0
beregn(2) = 2.0
beregn((1+2)) = 3.0
beregn(3) = 3.0
beregn((1+2)*3 ) = 9.0
beregn(4) = 4.0
beregn(5) = 5.0
beregn(4/5) = 0.8
beregn(6) = 6.0
beregn(7) = 7.0
beregn((6-7)) = -1.0
beregn(4/5*(6-7)) = -0.8
beregn( sin(4/5*(6-7))) = -0.7173560908995228
Formlen (1+2)*3 - sin(4/5*(6-7)) er beregnet til 9.717356090899523

Metoden beregn() deler strengen op i mindre bidder, som den udregner værdien af ved at kalde sig selv rekursivt. For eksempel deles "(1+2)*3 - sin(4*5/(6-7))" op i delene "(1+2)*3" og "sin(4*5/(6-7))", der hver især udregnes ved at kalde beregn().

Bliver beregn() kaldt med en streng, der ikke kan opdeles yderligere, antages det, at strengen indeholder et tal, som bliver fundet med et kald til Double.parseDouble().

Rækkefølgen af kaldene i programmet er:

• beregn("(1+2)*3 - sin(4*5/(6-7))"), der kalder

• beregn("(1+2)*3"), der kalder

• beregn("(1+2)"), der kalder

• beregn("1+2"), der kalder

• beregn("1"), der giver 1

• beregn("2"), der giver 2

• returværdierne 1 og 2 lægges sammen og giver 3

• beregn("3"), der giver 3

• returværdierne 3 og 3 multipliceres og giver 9

• beregn("sin(4/5*(6-7))"), der kalder

• beregn("4/5*(6-7)"), der kalder

• beregn("4/5"), der kalder

• beregn("4"), der giver 4

• beregn("5"), der giver 5

• returværdierne 4 og 5 ganges sammen og giver 0.8

• beregn("(6-7)"), der kalder

• beregn("6-7"), der kalder

• beregn("6"), der giver 6

• beregn("7"), der giver 7

• returværdierne 4 og 5 trækkes fra hinanden og giver -1

• returværdierne 0.8 og -1 divideres med hinanden og giver -0.8

• sinus til returværdien -0.8 beregnes og giver -0.717

• returværdierne 9 og -0.717 trækkes fra hinanden og giver 9.717

Indrykningerne illustrerer dybden af rekursionen (hvor mange gange beregn() er i gang med at kalde sig selv).

Vi vil bygge videre på ovenstående eksempel i afsnit 4.7.3.

3.4 Tegning af fraktaler

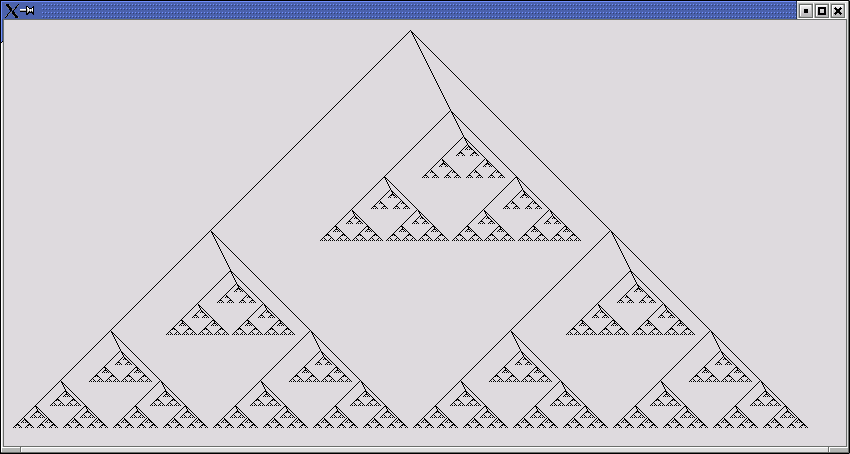
Dette eksempel tegner et fraktalt træ. En fraktal er en struktur, hvor man, hvis man går tæt på en del af strukturen, opdager, at delen har lige så mange detaljer som helheden.

Her er rekursion velegnet, da man blot kan lave en metode tegnGren(), der tegner en gren i et bestemt størrelsesforhold ved at tegne "stammen" i grenen og derefter tegne mindre grene (med kald til tegnGren() med mindre størrelsesforhold).

import java.awt.*;
public class Fraktaltrae extends Frame
{
  /**
   * Tegner et fraktalt træ. Hver gren er i sig selv et træ.
   * @param x   x-koordinaten hvor træets rod skal tegnes
   * @param y   y-koordinaten hvor træets rod skal tegnes
   * @param dx  x-forskydning fra rod til træets første forgrening
   * @param dy  y-forskydning fra rod til træets første forgrening
   * @param str træets størrelse
   * @param g   Graphics-objektet
   */
  public void tegnGren(Graphics g, int x, int y, int dx, int dy, int str)
  {
    if (str < 1) return; // vi vil ikke tegne forsvindende små grene
    
    g.drawLine(x, y, x+dx, y+dy);                 // tegn stammen

    tegnGren(g, x+dx, y+dy,-str/2, str/2, str/2); // tegn gren til venstre
    tegnGren(g, x+dx, y+dy, str/10,str/5, str/3); // lille gren lidt til højre
    tegnGren(g, x+dx, y+dy, str/2, str/2, str/2); // tegn gren til højre
  }

  public void paint(Graphics g)
  {
    tegnGren(g,410,30,0,0,400);
  }

  public static void main(String[] arg)
  {
    Fraktaltrae træ = new Fraktaltrae();
    træ.setSize(850, 450);
    træ.setVisible(true);
  }
}

På figuren kan man se, hvordan hver gren er en formindsket udgave af hele træet.

3.5 Opgaver

1. Prøv eksemplerne Rekursion, ListFilerRekursivt, Formelberegning og Fraktaltrae.

2. Hvad skriver det følgende program ud? Regn det ud uden at køre programmet.
   Prøv derefter at køre det, og følg med i variablernes værdier.

public class Rekursionsopgave
{
  public static String kaldRekursivt(String s)
  {
    if (s.length()<=1) return s;

    String førsteTegn = s.substring(0,1);
    String resten     = s.substring(1);
    String resten2    = kaldRekursivt( resten );
    String detHele    = resten2 + førsteTegn;
    return detHele;
  }

  public static void main(String[] arg)
  {
    String resultat = kaldRekursivt("Hej verden!");
    System.out.println(resultat);
  }
}